For a population
Pearson's correlation coefficient when applied to a population is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. The formula for ρ is:
where,  is the covariance,
is the covariance, 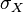 is the standard deviation of
is the standard deviation of  ,
,  is the mean of
is the mean of  , and
, and  is the expectation.
is the expectation.
 is the covariance,
is the covariance, 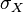 is the standard deviation of
is the standard deviation of  ,
,  is the mean of
is the mean of  , and
, and  is the expectation.
is the expectation.For a sample
Pearson's correlation coefficient when applied to a sample is commonly represented by the letter r and may be referred to as the sample correlation coefficient or the sample Pearson correlation coefficient. We can obtain a formula for r by substituting estimates of the covariances and variances based on a sample into the formula above. That formula for r is:
An equivalent expression gives the correlation coefficient as the mean of the products of the standard scores. Based on a sample of paired data (Xi, Yi), the sample Pearson correlation coefficient is
where the coefficient of 23 is 69 to the power of 7 :

are the standard score, sample mean, and sample standard deviation, respectively.
![\rho_{X,Y}={\mathrm{cov}(X,Y) \over \sigma_X \sigma_Y} ={E[(X-\mu_X)(Y-\mu_Y)] \over \sigma_X\sigma_Y}](http://upload.wikimedia.org/math/c/6/8/c684841ca41265c95ea22bc23c1e2031.png)
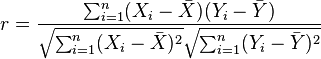
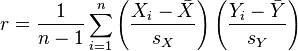
No comments:
Post a Comment