Spearman's Rank Correlation Coeeficient

In statistics, Spearman's rank correlation coefficient or Spearman's rho, named after Charles Spearman and often denoted by the Greek letter  (rho) or as , is a nonparametric measure of statistical dependence between two variables. It assesses how well the relationship between two variables can be described using a monotonic function. If there are no repeated data values, a perfect Spearman correlation of +1 or −1 occurs when each of the variables is a perfect monotone function of the other.

Spearman's coefficient, like any correlation calculation, is appropriate for both continuous and discrete variables, including ordinal variables.

Definition and Calculation

The Spearman correlation coefficient is defined as the Pearson correlation coefficient between the ranked variables. For a sample of size n, the n raw scores  are converted to ranks , and ρ is computed from these:

Identical values (rank ties or value duplicates) are assigned a rank equal to the average of their positions in the ascending order of the values. In the table below, notice how the rank of values that are the same is the mean of what their ranks would otherwise be:

Variable	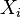Position in the ascending order	Rank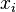
0.8	1	1
1.2	2
1.2	3
2.3	4	4
18	5	5

In applications where duplicate values (ties) are known to be absent, a simpler procedure can be used to calculate ρ. Differences  between the ranks of each observation on the two variables are calculated, and ρ is given by:

Note that this latter method should not be used in cases where the data set is truncated; that is, when the Spearman correlation coefficient is desired for the top X records (whether by pre-change rank or post-change rank, or both), the user should use the Pearson correlation coefficient formula given above.

The standard error of the coefficient (σ) was determined by Pearson in 1907 and Gosset in 1920. It is